The Wild East

In Einstein’s Special Theory of Relativity he poses that “the same laws of physics hold true in all inertial reference frames and that the speed of light is the same for all observers, even those moving with respect to one another. ” The best explanation I’ve seen for this is a YouTube video on non Euclidian Geometry (starts at 20:25) which likens an astronaut in the international space station looking at a pen that is floating in mid air to a painter and his bucket of paint on planet earth who fell off of a ladder. Both the astronaut and the painter are in free fall, only the painter will eventually meet a sudden and abrupt end. To each professional, their relative environment looks the same; they feel weightless, they’re looking at an object floating in front of their face. Their relative observations dictate that they are floating, not being acted upon by any outside force. Objectively, though, we know that they are both being acted on by the same laws of physics and are in free fall.

I was thinking about this theory while on my latest hike. While ascending Mt. Carrigain, in Livermore New Hampshire, I experienced the same distortion of time as I always do on longer, more strenuous hikes. My smart watch helps me keep track of time objectively but something odd happens relatively in my mind and body as the hike goes on. At first, time moves relatively quickly, then when I check my watch at what feel like equal time intervals the length of time which actually passed since my last check of the watch decreases. I’ll think 10 minutes passed at the bottom and I’m just about spot on. I think 10 minutes passed further up the trail and turns out my watch says only 5 have. On this hike, finally, I think found a unified theory of this time distortion that I and other hikers experience. Here’s my nerdy and uncessray Mountain Theory of Relativity brought to you by my mathematics degree and my love for the mountains.

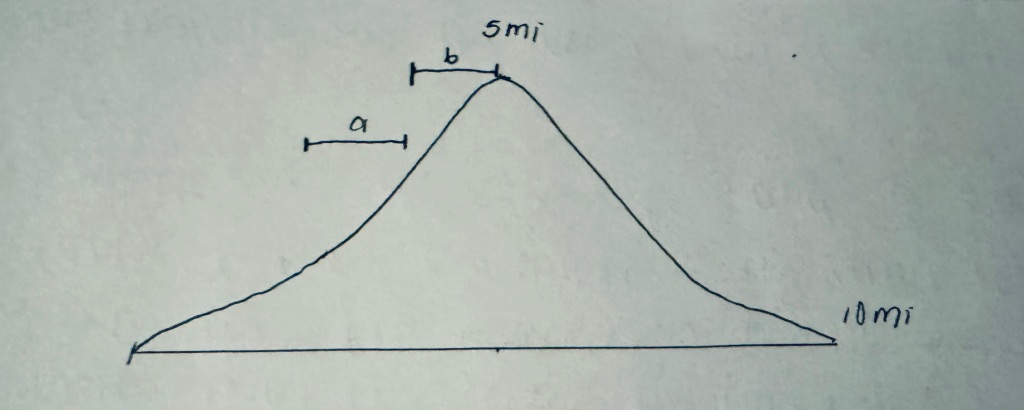
• Let a be the distance from 3.8 miles to 4.4 miles.
• Let b be the distance from 4.4 miles to the summit at 5 miles.
• Let t_e be the time elapsed since the start of the hike. Therefore t_e = 0 at the start and t_e at mile 10 is the total duration of the hike.
• Let t_rs be the time remaining until the hiker reaches the summit, objectively. Imagine we have the ability to see the future and we know what t_rs is for the hiker at any point in time during the ascent.
• Let t_ep be the time which is perceived to have elapsed by the hiker between any two points which they guess relatively without looking at their watch.

I hypothesize that the closer the hiker gets to the summit (t_rs -> 0) the different between t_e and t_ep grows by a factor of X where X is a positive real number.

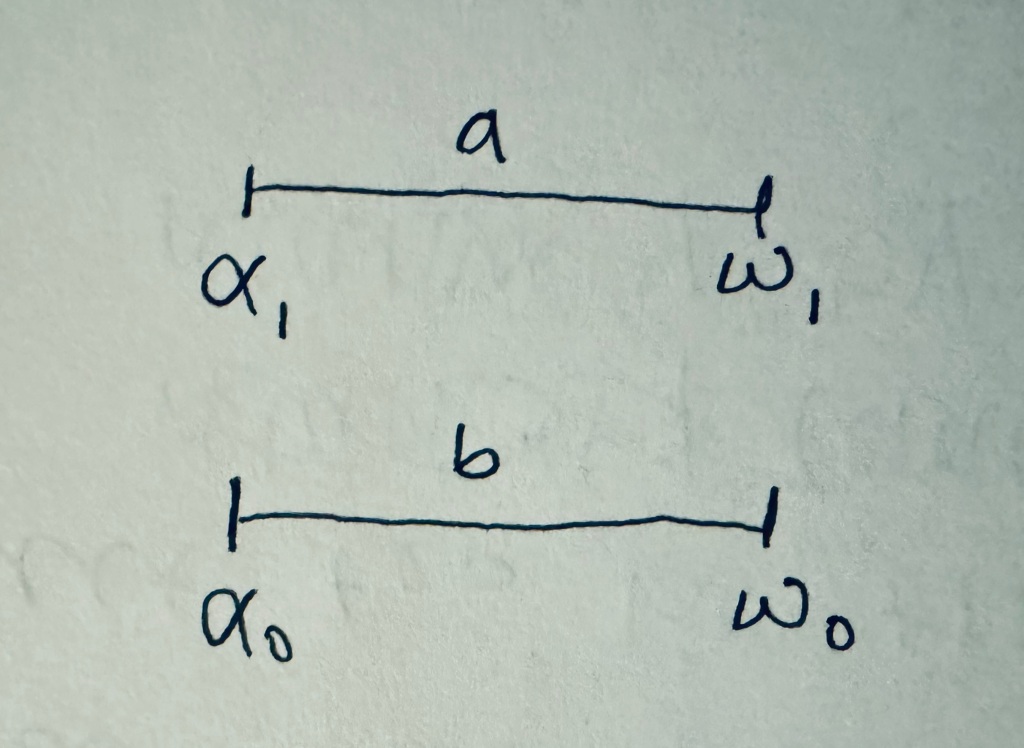
Ex. Take mile markers ⍺₀ and ⍵₀ which define segment b (shown below) and ⍺₁ and ⍵₁ which define segment a (shown below) which have the following properties

• ⍵₀ – ⍺₀ > 0
• ⍵₀ – ⍺₀ = ⍵₁ – ⍺₁
• ⍺₀ > ⍺₁
• ⍵₀ > ⍵₁

Defining some additional variables for our example let the following be true

• t_epa is the perceived time elapsed for the hiker on segment a
• t_epb is the perceived time elapsed for the hiker on segment b
• t_ea is the objective time elapsed for segment a
• t_eb is the objective time elapsed for segment b

Our Theory of Mountain Relativity would dictate that t_epa < t_epb when in reality t_ea = t_eb . In the case where t_ea ! = t_eb then t_ea / t_eb > t_epa / t_epb where t_ea < t_eb .

This explains why the last 0.6 miles is always the longest perceived stretch of the hike regardless of how long it actually takes.